ESTRUTURAS METÁLICAS E DE MADEIRA
Uma viga de madeira dicotiledônea com classe de resistência C20, possui dois balanços com comprimentos de 1,0 m cada e suporta parte de uma cobertura de varanda. Assim, qual é o valor limite para o deslocamento ocasionado em cada balanço dessa viga segundo a ABNT NBR 7190:1997, em centímetros?
Observação: o valor limite de deslocamento é o valor máximo que pode ser admitido para que não ocorra deformação excessiva na estrutura.
2,0 cm
1,5 cm
1,0 cm
2,5 cm
0,5 cm
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 16, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C40. Considerar classe de carregamento de longa duração e classe de umidade 4.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 57,6 kN.
Nd,res = 49,2 kN.
Nd,res = 122,9 kN.
Nd,res = 172,8 kN.
Nd,res = 144,3 kN.
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 6 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 12464 kN
Nd,res = 15973 kN
Nd,res = 11225 kN
Nd,res = 13660 kN
Nd,res = 18454 kN
Calcule o valor máximo limite para o deslocamento vertical (δlim) de uma viga de piso, biapoiada de alma cheia, conforme a ABNT NBR 8800:2008. A viga possui vão de 5 m, é contida lateralmente e não possui enrijecedores. Adotar aço MR250.
Perfil VS 600×111 kg/m:
d = 600 mm
h = 568 mm
tw = 8 mm
tf = 16 mm
bf = 300 mm
δmáx = 2,52 cm.
δmáx = 1,00 cm.
δmáx = 2,15 cm.
δmáx = 1,43 cm.
δmáx = 1,87 cm.
Uma placa de aço 12 mm, submetida à tração axial, está ligada a uma outra placa 12 mm formando um perfil T, por meio de solda de filete. Determinar o esforço resistente Rd da solda de filete, com ambos lados iguais a 6 mm. Considerar eletrodo E60 e aço MR250 (ASTM A36), e a ação como variável de utilização.
Adotar L = 150 mm. Resistência à ruptura da solda (E60): fw = 415 MPa.
Rd = 186 kN.
Rd = 232 kN.
Rd = 200 kN.
Rd = 217 kN.
Rd = 157 kN.
Duas chapas 400 mm × 20 mm são emendadas por traspasse, com parafusos d = 20 mm, sendo os furos realizados por punção. Determinar o valor mínimo para o esforço resistente de projeto das chapas (em kN), admitindo-as submetidas à tração axial. Considerar aço MR250 (A36).
2092 kN.
1962 kN.
1818 kN.
2000 kN.
1913 kN.
Efetuar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 22 kN
Carga acidental (de uso e ocupação): Q1 = 15 kN
Ação do vento de sobrepressão: Qv1 = 13 kN
Ação do vento de sucção: Qv2 = -6 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.
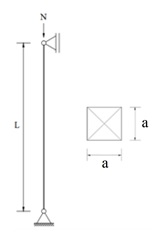
Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa
2,0 cm
1,5 cm
1,0 cm
2,5 cm
0,5 cm
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 16, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é dicotiledônea e serrada de 2ª categoria, com classe de resistência C40. Considerar classe de carregamento de longa duração e classe de umidade 4.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 57,6 kN.
Nd,res = 49,2 kN.
Nd,res = 122,9 kN.
Nd,res = 172,8 kN.
Nd,res = 144,3 kN.
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 6 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 12464 kN
Nd,res = 15973 kN
Nd,res = 11225 kN
Nd,res = 13660 kN
Nd,res = 18454 kN
Calcule o valor máximo limite para o deslocamento vertical (δlim) de uma viga de piso, biapoiada de alma cheia, conforme a ABNT NBR 8800:2008. A viga possui vão de 5 m, é contida lateralmente e não possui enrijecedores. Adotar aço MR250.
Perfil VS 600×111 kg/m:
d = 600 mm
h = 568 mm
tw = 8 mm
tf = 16 mm
bf = 300 mm

δmáx = 2,52 cm.
δmáx = 1,00 cm.
δmáx = 2,15 cm.
δmáx = 1,43 cm.
δmáx = 1,87 cm.
Uma placa de aço 12 mm, submetida à tração axial, está ligada a uma outra placa 12 mm formando um perfil T, por meio de solda de filete. Determinar o esforço resistente Rd da solda de filete, com ambos lados iguais a 6 mm. Considerar eletrodo E60 e aço MR250 (ASTM A36), e a ação como variável de utilização.
Adotar L = 150 mm. Resistência à ruptura da solda (E60): fw = 415 MPa.

Rd = 186 kN.
Rd = 232 kN.
Rd = 200 kN.
Rd = 217 kN.
Rd = 157 kN.
Duas chapas 400 mm × 20 mm são emendadas por traspasse, com parafusos d = 20 mm, sendo os furos realizados por punção. Determinar o valor mínimo para o esforço resistente de projeto das chapas (em kN), admitindo-as submetidas à tração axial. Considerar aço MR250 (A36).

2092 kN.
1962 kN.
1818 kN.
2000 kN.
1913 kN.
Efetuar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 22 kN
Carga acidental (de uso e ocupação): Q1 = 15 kN
Ação do vento de sobrepressão: Qv1 = 13 kN
Ação do vento de sucção: Qv2 = -6 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa
Nd,res = 57,6 kN.
Nd,res = 49,2 kN.
Nd,res = 122,9 kN.
Nd,res = 172,8 kN.
Nd,res = 144,3 kN.
Determine, de acordo com a ABNT NBR 8800:2008, o esforço normal de compressão resistente de cálculo (Nd,res) para a coluna soldada (CS) indicada na figura abaixo, cujo comprimento (L) é de 6 m. A coluna é simplesmente apoiada em relação aos dois eixos de análise.
Aço A-36 (MR250) Propriedades: fy = 25 kN/cm2; fu = 40 kN/cm2; E = 20000 kN/cm2.
Perfil CS 700x458 kg/m Propriedades:
d = 700 mm
h = 637 mm
tw = 22,4 mm
tf = 31,5 mm
bf = 700 mm

Em caso de resposta decimal, arredondar o número conforme o inteiro mais próximo.
Nd,res = 12464 kN
Nd,res = 15973 kN
Nd,res = 11225 kN
Nd,res = 13660 kN
Nd,res = 18454 kN
Calcule o valor máximo limite para o deslocamento vertical (δlim) de uma viga de piso, biapoiada de alma cheia, conforme a ABNT NBR 8800:2008. A viga possui vão de 5 m, é contida lateralmente e não possui enrijecedores. Adotar aço MR250.
Perfil VS 600×111 kg/m:
d = 600 mm
h = 568 mm
tw = 8 mm
tf = 16 mm
bf = 300 mm

δmáx = 2,52 cm.
δmáx = 1,00 cm.
δmáx = 2,15 cm.
δmáx = 1,43 cm.
δmáx = 1,87 cm.
Uma placa de aço 12 mm, submetida à tração axial, está ligada a uma outra placa 12 mm formando um perfil T, por meio de solda de filete. Determinar o esforço resistente Rd da solda de filete, com ambos lados iguais a 6 mm. Considerar eletrodo E60 e aço MR250 (ASTM A36), e a ação como variável de utilização.
Adotar L = 150 mm. Resistência à ruptura da solda (E60): fw = 415 MPa.

Rd = 186 kN.
Rd = 232 kN.
Rd = 200 kN.
Rd = 217 kN.
Rd = 157 kN.
Duas chapas 400 mm × 20 mm são emendadas por traspasse, com parafusos d = 20 mm, sendo os furos realizados por punção. Determinar o valor mínimo para o esforço resistente de projeto das chapas (em kN), admitindo-as submetidas à tração axial. Considerar aço MR250 (A36).

2092 kN.
1962 kN.
1818 kN.
2000 kN.
1913 kN.
Efetuar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 22 kN
Carga acidental (de uso e ocupação): Q1 = 15 kN
Ação do vento de sobrepressão: Qv1 = 13 kN
Ação do vento de sucção: Qv2 = -6 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa

Nd,res = 12464 kN
Nd,res = 15973 kN
Nd,res = 11225 kN
Nd,res = 13660 kN
Nd,res = 18454 kN
Calcule o valor máximo limite para o deslocamento vertical (δlim) de uma viga de piso, biapoiada de alma cheia, conforme a ABNT NBR 8800:2008. A viga possui vão de 5 m, é contida lateralmente e não possui enrijecedores. Adotar aço MR250.
Perfil VS 600×111 kg/m:
d = 600 mm
h = 568 mm
tw = 8 mm
tf = 16 mm
bf = 300 mm

δmáx = 2,52 cm.
δmáx = 1,00 cm.
δmáx = 2,15 cm.
δmáx = 1,43 cm.
δmáx = 1,87 cm.
Uma placa de aço 12 mm, submetida à tração axial, está ligada a uma outra placa 12 mm formando um perfil T, por meio de solda de filete. Determinar o esforço resistente Rd da solda de filete, com ambos lados iguais a 6 mm. Considerar eletrodo E60 e aço MR250 (ASTM A36), e a ação como variável de utilização.
Adotar L = 150 mm. Resistência à ruptura da solda (E60): fw = 415 MPa.

Rd = 186 kN.
Rd = 232 kN.
Rd = 200 kN.
Rd = 217 kN.
Rd = 157 kN.
Duas chapas 400 mm × 20 mm são emendadas por traspasse, com parafusos d = 20 mm, sendo os furos realizados por punção. Determinar o valor mínimo para o esforço resistente de projeto das chapas (em kN), admitindo-as submetidas à tração axial. Considerar aço MR250 (A36).

2092 kN.
1962 kN.
1818 kN.
2000 kN.
1913 kN.
Efetuar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 22 kN
Carga acidental (de uso e ocupação): Q1 = 15 kN
Ação do vento de sobrepressão: Qv1 = 13 kN
Ação do vento de sucção: Qv2 = -6 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa

δmáx = 2,52 cm.
δmáx = 1,00 cm.
δmáx = 2,15 cm.
δmáx = 1,43 cm.
δmáx = 1,87 cm.
Uma placa de aço 12 mm, submetida à tração axial, está ligada a uma outra placa 12 mm formando um perfil T, por meio de solda de filete. Determinar o esforço resistente Rd da solda de filete, com ambos lados iguais a 6 mm. Considerar eletrodo E60 e aço MR250 (ASTM A36), e a ação como variável de utilização.
Adotar L = 150 mm. Resistência à ruptura da solda (E60): fw = 415 MPa.

Rd = 186 kN.
Rd = 232 kN.
Rd = 200 kN.
Rd = 217 kN.
Rd = 157 kN.
Duas chapas 400 mm × 20 mm são emendadas por traspasse, com parafusos d = 20 mm, sendo os furos realizados por punção. Determinar o valor mínimo para o esforço resistente de projeto das chapas (em kN), admitindo-as submetidas à tração axial. Considerar aço MR250 (A36).

2092 kN.
1962 kN.
1818 kN.
2000 kN.
1913 kN.
Efetuar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 22 kN
Carga acidental (de uso e ocupação): Q1 = 15 kN
Ação do vento de sobrepressão: Qv1 = 13 kN
Ação do vento de sucção: Qv2 = -6 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa

Rd = 186 kN.
Rd = 232 kN.
Rd = 200 kN.
Rd = 217 kN.
Rd = 157 kN.
Duas chapas 400 mm × 20 mm são emendadas por traspasse, com parafusos d = 20 mm, sendo os furos realizados por punção. Determinar o valor mínimo para o esforço resistente de projeto das chapas (em kN), admitindo-as submetidas à tração axial. Considerar aço MR250 (A36).

2092 kN.
1962 kN.
1818 kN.
2000 kN.
1913 kN.
Efetuar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 22 kN
Carga acidental (de uso e ocupação): Q1 = 15 kN
Ação do vento de sobrepressão: Qv1 = 13 kN
Ação do vento de sucção: Qv2 = -6 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa

2092 kN.
1962 kN.
1818 kN.
2000 kN.
1913 kN.
Efetuar as possíveis combinações últimas normais (Estado Limite Último) para uma barra de treliça constituída por perfil de aço, sujeita a uma força axial de tração. Tal força é originada a partir das seguintes ações:
Peso próprio da estrutura de aço: G1 = 22 kN
Carga acidental (de uso e ocupação): Q1 = 15 kN
Ação do vento de sobrepressão: Qv1 = 13 kN
Ação do vento de sucção: Qv2 = -6 kN
Considerar que na construção não há predominância de pesos ou equipamentos que permanecem fixos por longos períodos de tempo, nem de elevadas concentrações de pessoas.
A partir das combinações determinadas, qual valor obtido para o esforço normal de tração será utilizado nas verificações de segurança quanto ao Estado Limite Último (ELU)? Em caso de resposta decimal, considerar uma casa após a vírgula.
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa
56,3 kN
68,4 kN
77,6 kN
73,9 kN
60,9 kN
A determinação da força crítica de flambagem é um procedimento muito importante para analisar o comportamento de estruturas sujeitas à compressão, como pilares e arcos. É com base no valor da força crítica de flambagem que é possível identificar inicialmente se o equilíbrio da estrutura será estável, neutro ou instável conforme as ações suportadas. Curiosamente, o conceito de força crítica de flambagem foi primeiramente desenvolvido por Euler ainda no século XVIII, quando o emprego de peças estruturais esbeltas ainda não era comum, pois somente com a revolução industrial e o advento do aço estrutural houve a objetivo de priorizar a esbeltez das estruturas. É possível afirmar que a contribuição de Euler para a engenharia estrutural foi essencial e muito à frente de seu tempo.
Dessa forma, determine a força crítica de flambagem (Fe) para o pilar de madeira indicado. O pilar é simplesmente apoiado segundo os dois planos de análise. A seção transversal é quadrada, com lado (a) de 20 cm. A barra possui comprimento (L) de 360 cm. Considerar madeira dicotiledônea serrada de 2ª categoria, classe de resistência C40, classe de carregamento de longa duração e classe de umidade 3.
Em caso de resposta decimal, considerar uma casa após a vírgula.

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa

Fe = 342,3 kN.
Fe = 443,5 kN.
Fe = 684,6 kN.
Fe = 1031,2 kN.
Fe = 887,0 kN.
Determinar o esforço normal de tração resistente para uma barra de madeira com seção transversal retangular, com dimensões 6 × 12, segundo os requisitos de segurança quanto ao Estado Limite Último (ELU). A madeira utilizada é conífera e serrada de 2ª categoria, com classe de resistência C20. Considerar classe de carregamento de longa duração e classe de umidade 2.
Em caso de resposta decimal, considerar uma casa após a vírgula.
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.
Calcular a resistência de cálculo no estado limite último da madeira Ipê (dicotiledônea) quanto à compressão paralela às fibras (fc0,d) e o módulo efetivo de elasticidade à compressão paralela às fibras (Ec0,ef), em MPa. Considerar carregamento de longa duração, classe de umidade 4 e madeira serrada de 2ª categoria. Valores médios adotados:
fc0,m = 76,0 MPa
Ec0,m = 18 011 MPa
Nd,res = 144,3 kN.
Nd,res = 122,9 kN.
Nd,res = 49,2 kN.
Nd,res = 57,6 kN.
Nd,res = 172,8 kN.